Question

Solve for C.
c = _ degrees

Answer 1

The value of
`\tt C =\boxed{ 32.68^o}`

Explanation:

Given:

Opposite side of C = c = 55

a = 90

b = 50

∡C = ?

Solution:

We can use the Law of Cosines to solve for C.

The Law of Cosines states that for a triangle with side lengths a, b and c and angle measure C opposite side c, the following equation holds:

`\boxed{\tt c^2 = a^2 + b^2 - 2ab \: cos C}`

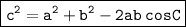
Substituting value,

`\tt 55^2 = 90^2 + 50^2 - 2 \cdot 90 \cdot 50 \: cos C`

Simplifying the left side of the equation, we get:

`\tt 3025 = 8100+2500- 9000 \:cos C`

`\tt 9000\: cosC = 8100+2500-3025`

`\tt 9000\: cosC= 7575`

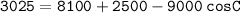
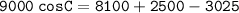
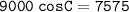
Solving for cos C, we get:

`\tt cos C = (7575)/(9000)`

`\tt cos C = (101)/(120)`

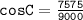
The angle measure C is the arc cosine of
`\tt (101)/(120)` .

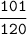Using the calculator and rounding to the nearest tenth, we get:

`\tt C = cos^(-1) ((101)/(120))= 32.68^o`

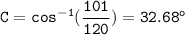
Therefore, the value of C is 32.68 degrees.