Question

In the following diagram, a circle is inscribed in a square. How can you find the area of the shaded region?

Notice that the shaded region of the figure is composed of four identical pieces. However, each piece has a curved side, which makes it very difficult to find its area using a direct method. In this type of diagram, the easiest way to find the area uses an indirect method.
Look at the diagram using a different perspective. The shaded region is composed of four identical pieces. OR, the shaded region is the area of the square minus the area of the circle. Since you know how to find the area of both a square and a circle, this is a much easier method for solving!
Area of square: s? = (6 )2 = 36 cm?
Area of circle: 2 ~ (3.14) (3 cm)? ~ (3.14) (9 cm?) ~ 28.26 cm
2
Area of shaded region: 36 cm?
_ 28 26 cm? = 7.74 cm?
The area of the shaded region is approximately 7.74 square centimeters.
Answer the questions based on the following diagram. Note: The two triangles meet at the center of the circle. 1. What is the approximate area of the circle? Use 3.14 in your calculation.
2. What is the area of one of the triangles?
3. What is the approximate area of the shaded region of the diagram?
1. approximate area of the circle:
mm?
2. area of one of the triangles.
mm?
3. approximate area of the shaded region of the diagram:
mm?

Answer 1

Approximate area of the circle: 254.34mm².

Approximate area of the triangle: 40.5mm².

Approximate area of the shaded region: 173.34mm².

Explanation:

From the diagram, it appears that two isosceles right triangles meet at the center of a circle with radius 9.

The area of a circle can be expressed as
`\pi r^2`, so the area of this circle is
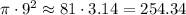`\pi\cdot9^2\approx 81\cdot3.14=254.34` mm².

The area of each of the isosceles right triangles is
`9^2/2=40.5` mm².

The area of the shaded region is then the total area of the circle minus the total area of the triangles (since there are two, their total area is 81), which is then
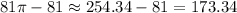`81\pi-81\approx254.34-81=173.34` mm².

Answer 2

1 area of one triangle is 40.5square mm

2 area of the shaded region is 173.34 square mm

3 area of the circle is 254.34 square mm

Explanation:

simple