Question

A certain number is 3 more than twice another. If their sum is increased by 8, the result is 41. Find the numbers.

Answer 1

the two numbers are 16.5 and 3.67

Explanation:

let the numbers be x and y

according to the question,

x = 3 + y² (1)

x + 3 + y² + 8 = 41

x + y² = 41 - 11

x + y² = 30

y² = 30 - x (2)

by substituting the value of y² from eq(2) into eq(1)

x = 3 + 30 - x

2x = 33

x = 33/2 = 16.5

thus,

y² = 30 - 16.5 = 13.5

y = 3.67

Answer 2

• 10 and 23

Step-by-step explanation:

Let The first number be x. If, a certain number is 3 more than twice another.

Then the another number will be,

3 + 2x - - - (Eqn. 1)

Sum of both the numbers,

`\sf x + 3 + 2x`

`\sf 3x + 3`

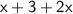
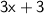
Now, If their sum is increased by 8, the result is 41.

`\sf 3x + 3 + 8 = 41`

`\sf 11 + 3x = 41`

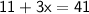
Subtract 11 from both sides,

`\sf11 + 3x - 11 = 41 - 11`

`\sf 3x = 30`

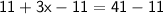
Divide both sides by 3,

`\sf x = 10`

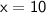
Since First number is x = 10

Substituting the value of x in eqn. 1, we have,

`\sf Second \: number = 3 + 2x \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: = \sf 3 + 2(10) \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \sf = 3 + 20\\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \sf = 23`

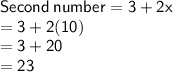
So The second number is 23.

Therefore, The two required numbers are 10 and 23.