Question

What is the smallest positive integer divisible by integers $1$ through $99$?

Answer 1

64×81×25×49×11×13×···×89×97.

Explanation:

The smallest positive integer divisible by the integers 1 through 99 will be the least common multiple (LCM) of the integers 1-99.

We then must find the largest power of all the primes up to 99 appearing in any of the integers up to 99.

For 2, the largest power is
`2^6=64`.

For 3, the largest power is
`3^4=81`.

For 5, the largest power is 5² = 25.

For 7, the largest power is 7² = 49.

For all primes p in 11-97, the largest power is p.

So, the LCM of all the numbers is then
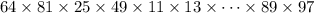`64*81*25*49*11*13*\cdots*89*97`.

Answer 2

1

Explanation:

the smallest positive integer divisible by integers 1 through 99 will be 1