Question

Show that the four points (2,3), (5,8), (0,5) and (-3,0) are the vertices of a rhombus​

Answer 1

In order to show that the four points (2,3), (5,8), (0,5), and (-3,0) are the vertices of a rhombus, we need to demonstrate two conditions:

1. All sides of the quadrilateral are equal in length.

2. The opposite sides are parallel to each other.

Let's calculate the distance between each pair of points to check the first condition by using Formula:

`\boxed{\tt d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)}`

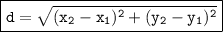
where:

• d is the distance between the two points
• (x1, y1) are the coordinates of the first point
• (x2, y2) are the coordinates of the second point

Distance between (2,3) and (5,8):

`\tt d_1 = √((5 - 2)^ + (8 - 3)^2)=√(3^2 + 5^2)=√(34)`

Distance between (5,8) and (0,5):

`\tt d_2 = √((0 - 5)^2 + (5 - 8)^2)= √(25 + 9) = √(34)`

Distance between (0,5) and (-3,0):

`\tt d_3 = √((-3 - 0)^2 + (0 - 5)^2)= √(9+25) = √(34)`

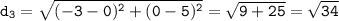
Distance between (-3,0) and (2,3):

`\tt d_4 = √((2 -(-3))^2 + (3-0)^2)= √(25 + 9) = √(34)`

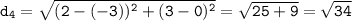
As all four distances (d₁, d₂, d₃, and d₄) are equal to
`√(34)`, the first condition is satisfied.

Next, let's check the slopes of the sides to verify the second condition (opposite sides are parallel) by using slope formula:

`\boxed{\tt m =( (y_2 - y_1))/((x_2 - x_1))}`

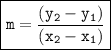
where:

• m is the slope of the line
• (x1, y1) are the coordinates of the first point on the line
• (x2, y2) are the coordinates of the second point on the line

Slope of the line passing through (2,3) and (5,8):

`\tt m_1 = ((8 - 3) )/((5 - 2))=(5)/(3)`

Slope of the line passing through (0,5) and (-3,0):

`\tt m_2 = ((0-5) )/((-3-0))=(5)/(3)`

Slope of the line passing through (5,8) and (0,5):

`\tt m_3 = ((5-8) )/((0-5))=(3)/(5)`

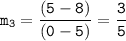
Slope of the line passing through (-3,0) and (2,3):

`\tt m_4= ((3 - 0) )/((2 - (-3)))=(3)/(5)`

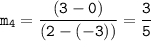
Since opposite sides have equal slopes (m₁ = m₂ and m₃ = m₄), they are parallel, and the second condition is satisfied.

Since both conditions are met, we can conclude that the four points (2,3), (5,8), (0,5), and (-3,0) are the vertices of a rhombus.

SHOWED