Question

A cat 20 cm tall is located 35 cm from the diverging lens of focal length 5 cm. What is the height of the image?

Answer 1

`h_i=2.5 \ cm`

Step-by-step explanation:

To determine the height of the image formed by a diverging lens, we can use the lens formula:

`\rightarrow (1)/(f)=(1)/(d_0)+(1)/(d_i)`

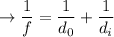
Where:

• "f" is the focal length of the lens

• "d₀" is the object distance (distance of the object from the lens)

• "dᵢ" is the image distance (distance of the image from the lens)

We are given:

`f=-5 \cm \ \text{(negative because it's a diverging lens)}\\\\d_0=35 \ cm`

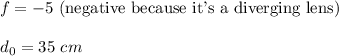
To find "dᵢ," we rearrange the lens formula:

`\Longrightarrow \boxed{(1)/(d_i)=(1)/(f)-(1)/(d_0)}`

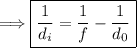
Now, let's calculate dᵢ:


`\Longrightarrow (1)/(d_i)=(1)/(-5)-(1)/(35)\\\\\\\\\Longrightarrow (1)/(d_i)=-(8)/(35)`

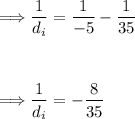
Now, taking the reciprocal of both sides to find dᵢ:

`\Longrightarrow d_i=-(35)/(8)\\ \\\\\\\therefore d_i=-4.375 \ cm`

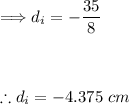
The negative sign indicates that the image is virtual (it is formed on the same side as the object, in this case, the opposite side of the lens).

Now, to find the height of the image, we can use the magnification formula:

`\rightarrow m=(h_i)/(h_o)=-(d_i)/(d_0)`

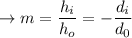
where:

"h₀" is the height of the object, which is 20 cm.

Substitute the values:

`\Longrightarrow(h_i)/(20)=-(-4.375)/(35)\\\\\\\\\Longrightarrow(h_i)/(20)=0.125\\\\\\\\\Longrightarrow h_i=0.125(20)\\\\\\\\\therefore \boxed{\boxed{h_i=2.5 \ cm}}`

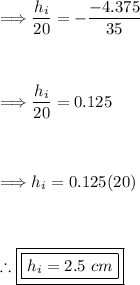
So, the height of the image is 2.5 cm.