Question

In a recent season of the TV show Survivor, 16 players were split into two teams of 8 players each. One player on each team was randomly given a secret idol which would not have a power until later in the game. The teams then competed in challenges every few days with each team equally likely to win each challenge. The losing team would then lose a random player. What is the probability (as a fraction) that, when 10 players remain, both players with a secret idol are still in the game?

Answer 1

The probability that both players with a secret idol are still in the game is 47/128.

Explanation:

We can split this problem into cases, based on the numbers of times in which a certain team (let us call them A and B) wins.

Case 1: Team A does not lose.

All eliminated players are from team B. The chance that a secret idol is not eliminated is
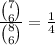`\frac{\tbinom{7}{6}}{\tbinom{8}{6}}=(1)/(4)`. (There are 8C6 ways to choose 6 members to be eliminated, and 7C6 ways to choose 6 members to be eliminated such that the idol is not). Because the probability that team A does not lose is
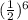`((1)/(2))^6`, the probability that this case contributes is
`(1)/(4)*(1)/(64)=(1)/(256)`.

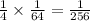Case 2: Team A loses once.

Using a similar reasoning to the previous part, the chance that an idol is not eliminated from team A is 7/8, and the chance that an idol is not eliminated from team B is 3/8. The probability that this case contributes is then
`\tbinom{6}{1}*(7)/(8)*(3)/(8)*(1)/(64)=(63)/(2048)`.

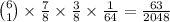Case 3: Team A loses twice.

Using a similar reasoning to the previous part, the chance that an idol is not eliminated from team A is 3/4, and the chance that an idol is not eliminated from team B is 1/2. The probability that this case contributes is then
`\tbinom{6}{2}*(3)/(4)*(1)/(2)*(1)/(64)=(45)/(512)`.

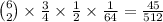Case 4: Team A loses three times.

Using a similar reasoning to the previous part, the chance that an idol is not eliminated from team A is 5/8, and the chance that an idol is not eliminated from team B is 5/8. The probability that this case contributes is then
`\tbinom{6}{3}*(5)/(8)*(5)/(8)*(1)/(64)=(125)/(1024)`.

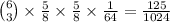Case 5: Team A loses four times.

Using a similar reasoning to the previous part, the chance that an idol is not eliminated from team A is 1/2, and the chance that an idol is not eliminated from team B is 3/4. The probability that this case contributes is then
`\tbinom{6}{4}*(1)/(2)*(3)/(4)*(1)/(64)=(45)/(512)`.

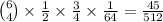Case 6: Team A loses five times.

Using a similar reasoning to the previous part, the chance that an idol is not eliminated from team A is 3/8, and the chance that an idol is not eliminated from team B is 7/8. The probability that this case contributes is then
`\tbinom{6}{5}*(3)/(8)*(7)/(8)*(1)/(64)=(63)/(2048)`.

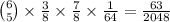Case 7: Team A loses six times.

Using a similar reasoning to the previous part, the chance that an idol is not eliminated from team A is 1/4. The probability that this case contributes is then
`\tbinom{6}{6}*(1)/(4)*(1)/(64)=(1)/(256)`.

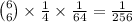Now, adding all of the probabilities together, the answer is
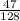`(47)/(128)`.