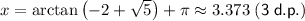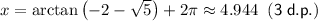Solve 4tanx/1-tan^2x=1 for 0 ≤ x ≤ 2π

Question

asked Jun 13, 2024 52.3k views

1 Answer

Justanoob · Answer 1 · 2024-06-19T07:35:22+0000

Answer:

x = 0.232, 1.803, 3.373, 4.944

Explanation:

Given trigonometric equation:

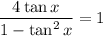
$(4 \tan x)/(1- \tan^2x)=1$

Multiply both sides of the equation by 1 - tan²x:

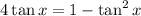
$4\tan x = 1 - \tan^2 x$

Add tan²x - 1 to both sides:

$\tan^2x+4\tan x-1=0$

Solve the quadratic equation by using the quadratic formula.

$\boxed{\begin{array}{c}\underline{\sf Quadratic\;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\quad\textsf{when}\;ax^2+bx+c=0\\\\\end{array}}$

In this case:

Substitute the values of a, b and c into the quadratic formula and solve for tan(x):

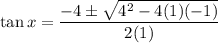
$\tan x=(-4\pm √(4^2-4(1)(-1)))/(2(1))$

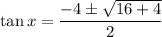
$\tan x=(-4\pm √(16+4))/(2)$

$\tan x=(-4\pm √(20))/(2)$

$\tan x=(-4\pm √(2^2 \cdot 5))/(2)$

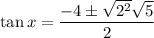
$\tan x=(-4\pm √(2^2) √(5))/(2)$

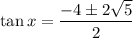
$\tan x=(-4\pm2√(5))/(2)$

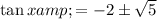
$\tan x&=-2\pm√(5)$

So the two solutions for tan(x) are:

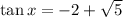
$\tan x=-2-√(5)$

$\tan x=-2+√(5)$

Solve for x by taking the arctan of both solutions, remembering that the tangent function is periodic with a period of π.

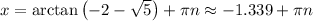
$x=\arctan\left(-2-√(5)\right)+\pi n\approx-1.339+\pi n$

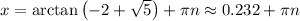
$x=\arctan\left(-2+√(5)\right)+\pi n \approx0.232+\pi n$

Therefore, the solutions for x that fall within the given interval 0 ≤ x ≤ 2π are:

$x=\arctan\left(-2+√(5)\right) \approx0.232\; \sf (3\;d.p.)$

$x=\arctan\left(-2-√(5)\right)+\pi \approx 1.803 \; \sf \;(3\;d.p.)$

$x=\arctan\left(-2+√(5)\right)+\pi \approx 3.373\; \sf (3\;d.p.)$

$x=\arctan\left(-2-√(5)\right)+2\pi \approx 4.944\; \sf \;(3\;d.p.)$