Question

A wizard in training has 300 grams of 20% liquid-gold solution. He wishes to drain some and replace it with an 80% solution so that he gets 300 grams of 35% solution. How many grams should the wizard drain and replace with 80% solution?

Answer 1

The wizard should drain 5x = 75g of solution.

Explanation:

The number of grams of gold in the original solution is 300*0.20=60g.

After the wizard drains some of the solution, let us say that he will be left with 60-x grams of gold and 300-5x grams of solution. Because he is replacing all of the lost solution with 80% solution, after he replaces the lost solution (which weighs 5x grams), he will have 60-x+4x = 60+3x grams of gold and 300 grams of solution.

We then wish to find x such that
`(60+3x)/(300) = .35`. Solving this equation, we find that x=15. The wizard should drain 5x = 75g of solution.

Answer 2

75 grams

Explanation:

Let's call the amount of the 20% liquid-gold solution the wizard drains of solution as "x" grams.

Note: A wizard had only 20% liquid gold solution,

Drain amount of gold =20% of x grams = 0.2x grams

Initial amount of gold = 20% of 300 grams = 0.2 * x= 60 grams

Final amount of gold = 35% of 300 grams = 0.35 * 300 = 105 grams

Replacement amount of gold = 80% of solution = 0.80*x = 0.8x grams

The equation for the amount of gold in the solution after the changes is:

initial gold - drained gold + replacement gold = final gold

60 - 0.2x + 0.8x = 105

Combine the like terms

0.6x= 105 - 60

0.6 x = 45

Divide by -0.2 to isolate "x":

`\tt x = (45 )/(0.6)`

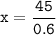
x = 75

Since grams should be in positive,

so, x = 75

The wizard should drain 75 grams of the 20% liquid-gold solution and replace it with an 80% liquid-gold solution.