Question

Solve absolute value equation 1 /2 = 1 /3 − |((x − 3) /6) + x|

Answer 1

No solution

Explanation:

To solve the given absolute value equation, we need to isolate the absolute value expression and consider two cases: one when the expression inside the absolute value is positive and another when it is negative. Let's break down the solution.

Our given equation:

`\frac12 = \frac13 - \Big| (x - 3)/(6) + x\Big|`

`\hrulefill`
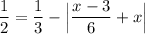
Start by isolating the absolute value expression on one side of the equation:

`\Longrightarrow \frac12 = \frac13 - \Big| (x - 3)/(6) + x\Big|`

Add the absolute value expression to each side of the equation, we get:

`\Longrightarrow \frac12 + \Big| (x - 3)/(6) + x\Big|= \frac13 - \Big| (x - 3)/(6) + x\Big|+\Big| (x - 3)/(6) + x\Big|\\\\\\\\\Longrightarrow \boxed\frac12 +\Big`

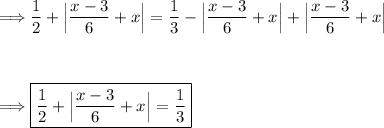
Subtract the value, 1/2, from either side of the equation:

`\Longrightarrow \frac12 - \frac12 +\Big| (x - 3)/(6) + x\Big| = \frac13-\frac12\\\\\\\\\ \Longrightarrow \boxed = -\frac16`

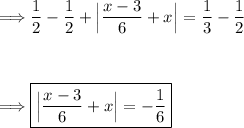
At this point, we have a problem since the absolute value of any real number is always non-negative (greater than or equal to zero), but we have -1/6 on the right side, which is negative. Therefore, there are no solutions to this equation.