Answer:
a) Amplitude: 1
b) 360
c) Maximum value for y: 3
d) Minimum value for y: 1
e) ℝ (all real numbers)
f) 1 ≤ y ≤ 3
g) y = 2
h) y = sin(x) + 2
Explanation:
a) A wave's amplitude is the distance from its center line to its peak.
From the graph, we can see that the wave's center line is y = 2, and the greatest y-value that the wave reaches is 3. Hence,
Amplitude = 3 - 2 = 1
b) A wave's period is the length on the x-axis that it takes to complete a full wave (up from the center line, down, then back up to the center line). We can identify this as 360.
c) We already established that the greatest y-value reached by the wave is 3.
d) We can see that the smallest y-value reached by the wave is 1.
e) The domain of a function is the set of x-values for which there is a real output — in other words, where there is a point on the graph. We can assume that this graph goes on forever to the left and right, so its domain is all real numbers, or ℝ.
f) The range of a function is the set of its outputs, or y-values. We can see that this graph goes from y = 1 to y = 3, so its range is 1 ≤ y ≤ 3.
g) In this case, "axis of the curve" most likely refers to the wave's center line, which is y = 2.
h) To form the equation for this wave, we can use the form:

where
 is the wave's amplitude,
is the wave's amplitude,
 a derivative of the wave's period (
a derivative of the wave's period (
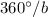 ),
),
 is the wave's horizontal shift, and
is the wave's horizontal shift, and
 is the wave's vertical shift.
is the wave's vertical shift.
We can assign the following variable values:
Finally, we can form the equation by plugging in these variable values:

