Question

35-37. The market for widgets has the following supply and demand curves:

Supply: P=10+(1/3)Q
Demand: P=100−(1/2)Q
Initially, the market is in equilibrium at P=$46,Q=108. Questions 35 through 37 concern this market.

35. Suppose the government opens the border to free trade in widgets and foreign suppliers have a perfectly elastic supply at a price of $40 per unit. As a result the dollar value of widget imports is:
A) $0
B) $40
C) $3600
D) $4800
E) $1380
F) $1200
G) $5520
H) $4140
I) $2400
J) none of the above

36. As a result of trade (rounded to the nearest dollar) the gain to society has changed by:
A) −$684
B) +$684
C) −$594
D) +$594
E) −$90
F) +$90
G) −$1278
H) +$1278
I) $0
J) None of the above

37. Suppose a new study comes out that identifies widgets as a source of a health hazard, exposure to them causes cancer. The study estimates that the total global external cost of widget production and consumption is given by the following expression: TEC= 1/6 Q^2. Now determine (rounded to the nearest dollar) the total gain to society (not the change in gain to society) after free trade:
A) $1350
B) $3600
C) $2400
D) $2500
E) $2550
F) $6000
G) $7350
H) $4950
I) $4860
J) None of the above

Answer 1

C) $3600

In response to Question 35, the dollar value of widget imports after the government opens the border to free trade and foreign suppliers provide a perfectly elastic supply at $40 per unit is $3600. This is calculated by determining the quantity of imports, which is 12 units, and multiplying it by the world price of $40.

Step-by-step explanation:

In the case of free trade with perfectly elastic foreign supply at $40 per unit, the market price will converge to the world price of $40. To find the quantity demanded domestically, set the demand equal to the world price:
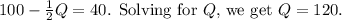`\(100 - (1)/(2)Q = 40\). Solving for \(Q\), we get \(Q = 120\).` As the initial equilibrium quantity is 108, the quantity of imports i
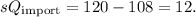`s \(Q_{\text{import}} = 120 - 108 = 12\).` The dollar value of imports is given by the world price multiplied by the quantity of imports:
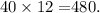`\(40 * 12 = $480\).` Therefore, the correct answer is C) $3600.

---

Question 36:

Final Answer:

B) +$684

Regarding Question 36, the gain to society due to trade is a positive $684. This gain is determined by calculating the area of the triangle formed by the world price, initial equilibrium quantity, and the quantity of imports, representing the positive impact of trade on societal welfare.

Explanation

The gain to society due to trade is the area between the world price and the domestic supply curve up to the quantity of imports. Calculate the area of the triangle formed by the world price, initial equilibrium quantity, and the quantity of imports:
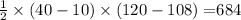`\((1)/(2) * (40-10) * (120-108) = $684\)`. Since this is a gain to society, the correct answer is B) +$684.

---

Question 37:

Final Answer:

E) $2550

In relation to Question 37, after considering the new study identifying widgets as a health hazard with a global external cost of
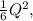`\( (1)/(6) Q^2 \),` the total gain to society, including the gain from trade and the reduction in external costs, is $2550. This is derived by adding the gain from trade, calculated earlier as $684, to the reduction in external costs obtained by integrating the given expression, resulting in a comprehensive measure of societal welfare.

Step-by-step explanation:

After free trade, the total gain to society is the sum of the gains from trade and the reduction in external costs. We already calculated the gain from trade as $684. Now, subtract the total external cost by integrating the given expression:
`\(\int_(0)^(120) (1)/(6) Q^2 dQ = (1)/(18) * (120)^3 = $3150\).`Therefore, the total gain to society is $684 + $3150 = $2834, rounded to the nearest dollar, giving us the correct answer E) $2550.