Question

Find the equation of the line passing through the point (-1,3) and is perpendicular to 3x + 2y = 6. Give your answer in slope-intercept form.

Answer 1

Here is the answer with the method. Lmk if u have any questions:)

Answer 2

`\boxed{\boldsymbol{y=(2)/(3)x+(11)/(3)}}`

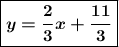
How to Solve:

Hi there!

The question is asking us to find the equation of the line. We're given the following pieces of information:

• The line is perpendicular to 3x + 2y = 6.
• It passes through the point (-1,3).

`\rule{350}{1}`

I am going to begin by writing the equation of the line 3x + 2y = 6 in slope-intercept form.

Slope-intercept form is y = mx + b, where:

• m = slope
• b = y-intercept
• (x,y) is a point on the line

Our equation again:

`\boldsymbol{3x+2y=6}`

First, I subtract 3x from each side:

`\boldsymbol{2y=6-3x}`

Then, I divide each side by 2:

`\boldsymbol{y=(6-3x)/(2)}`

`\boldsymbol{y=(6)/(2)-(3x)/(2)}`

`\boldsymbol{y=3-(3)/(2)x}`

`\boldsymbol{y=-(3)/(2)x-3}`

`\rule{350}{1}`

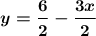
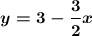
Now that we have our equation, we will determine the slope on the line that is perpendicular to it.

Recall that perpendicular lines have slopes that are opposite reciprocals.

The opposite reciprocal of -3/2 is:

• 2/3

We're also given that the line passes through (-1,3), so we substitute both the slope and the point into point-slope form:

`\boldsymbol{y-y_1=m(x-x_1)}`

`\boldsymbol{y-3=(2)/(3)(x-(-1)}`

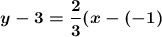
Simplify:

`\boldsymbol{y-3=(2)/(3)(x+1)}`

`\boldsymbol{y=(2)/(3)x+(2)/(3)+3}`

`\boldsymbol{y=(2)/(3)x+(2)/(3)+(3)/(1)}`

`\boldsymbol{y=(2)/(3)x+(2)/(3)+(9)/(3)}`

`\boldsymbol{y=(2)/(3)x+(11)/(3)}`

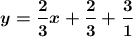
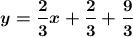
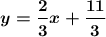
Therefore, the equation is
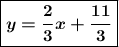`\boxed{\boldsymbol{y=(2)/(3)x+(11)/(3)}}`.