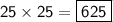Question

The sum of two numbers is 50. The maximum product is:__________ 450 625 565 850

Answer 1

Hello!

Answer:

`\Large \boxed{\sf 625}`

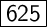
Explanation:

Let x and y be the two numbers.

So we have this equation:

`\sf x + y = 50`

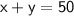
We want to maximize xy. The question translates to finding the maximum of the function f defined by:

`\sf f(x) = x (50 - x)`

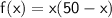
Simplify the function:

`\sf f(x) = 50 x - x^(2)`

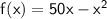
The graph of the function f is a concave down parabola. The maximum of f occurs at the vertex.

To find the vertex, we equate
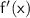`\sf f^(\prime)(x)` to 0, and we get:

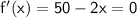`\sf f^(\prime) (x) = 50 - 2x = 0` if only
`\sf x = 25`

Using the first equation, we get:

`\sf x = y = 25`

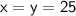
So the maximum product is:

`\sf 25 * 25 = \boxed{\sf 625}`