Question

The linear system x-y= -5 and x+y=1 has how many solutions

Answer 1

Explanation:

x-y= -5 eq.1

x+y=1 eq.2

Add two equations

2x = -4

divide both sides by 2

x = -2

To get the value of y, substitute x =-2 to any of the equations.

x-y=-5

-2-y=-5

-y=-3

y=3

Answer 2

(-2,3)

Explanation:

The question is asking us to find how many solutions this system has.

In order to answer that, I am going to solve the system. There are several methods for solving systems:

1. Graphing - you graph the equations; the point where they intersect is the solution to the system.
2. Substitution - you solve the equation for one variable and then plug it into the other equation.
3. Elimination - you eliminate one of the variables and subtract the two equations.

Our system is

`\begin{cases}\sf{x-y=-5}\\\sf{x+y=1}\end{cases}`

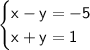
I am going to solve the first equation for x:

`\sf{x-y=-5}`

Add y to both sides:

`\sf{x=-5+y}`

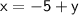
Now, plug in -5 + y into the second equation (instead of x)

`\sf{x+y=1}`

`\sf{-5+y+y=1}`

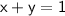
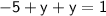
Combine like terms (y + y):

`\sf{-5+2y=1}`

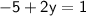
Add 5 to each side:

`\sf{2y=1+5}`

`\sf{2y=6}`

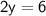
Divide each side by 2:

`\sf{y=3}`

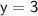
Now that we know the solution for y, plug in 3 into any of the equations to find x:

`\sf{x-y=-5}`

`\sf{x-3=-5}`

`\sf{x=-5+3}`

`\sf{x=-2}`

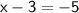
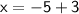
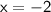
Therefore, the solution is (-2, 3)