Question

The Equation of the Line that Passes through the Points (2, −1) and (4, 5)

Answer 1

y = 3x -7

Explanation:

y = mx + b

To write the equation we need the m (slope) and the b (y-intercept).

m (slope):

The slope is the change in y over the change in x. We find the change by subtracting.

The y values are 5 and -1 (2,-1), (4,5).

The x values are 4 and 2 (2, -1), (4,5).

`(5-(-1))/(4-2)` =
`(5+1)/(2)` =
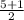`(6)/(2)` = 3

The m (slope) is 3.

b (y-intercept):

We will use the x and y values from one of the points (let's use the point (4,5) and the slope of 3 to solve for b

y = mx + b

5 = 3(4) + b

5 = 12 +b Subtract 12 from both sides

-7 = b

The b (y-intercept) is -7.

y = mx + b

substitute 3 for m and -7 for b

y = 3x -7

Helping in the name of Jesus.

Answer 2

Explanation:

Using the formula to find slope

m = (5--1)/(4-2)

m = 6/2

m = 3

General form of the linear equation is y =mx + b

use one of the 2 points and the slope and substitute to the general form

let's use (4,5)

y = mx + b

5 = 3(4) + b

5 = 12 + b

b = -7

Now you have the slope and y-intercept

The equation of the line that passes through the Points (2, −1) and (4, 5) is

y = 3x -7