Question

Please answer QUICKLY!!!

Answer 1

`(\bar x , \bar y)=\Big((8)/(5), \ 1 \Big)`

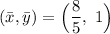
Explanation:

To find the exact coordinates of the centroid of the region bounded by the curves y = √x and y = (1/2)x on the interval 0 ≤ x ≤ 4, we'll use the techniques from Calculus 2, specifically the method of finding centroids of 2D shapes.

The centroid of a region bounded by two curves y = f(x) and y = g(x) on the interval [a, b] is given by:


`\rightarrow(\bar x, \bar y)= \Big((1)/(A) \displaystyle\int\limits^b_a {x[f(x)-g(x)]} \, dx ,(1)/(A) \displaystyle\int\limits^b_a {(1)/(2) [f(x)^2-g(x)^2]} \, dx\Big)`

where A is the area of the region between the curves f(x) and g(x), and it is given by:

`\rightarrow A = \displaystyle \int\limits^b_a {[f(x)-g(x)]} \, dx`

`\hrulefill`

Let's start by finding the area (A) of the region first, using the power rule for integration:

`\Longrightarrow A = \displaystyle \int\limits^4_0 {[√(x) -(1)/(2)x ]} \, dx \\\\\\\\\Longrightarrow A = \displaystyle \int\limits^4_0 [x^{(1)/(2) } -(1)/(2)x ]} \, dx \\\\\\\\\Longrightarrow A = \Big[(2)/(3)x^{(3)/(2)}-(1)/(4) x^2 \Big]\limits^4_0\\\\\\\\\Longrightarrow A = \Big[(2)/(3)(4)^{(3)/(2)}-(1)/(4)(4)^2 \Big]-[0]\\\\\\\\\Longrightarrow A = \Big[(16)/(3) -4 \Big]\\\\\\\\\therefore A = (4)/(3)`

Now, let's find the x-coordinate of the centroid:

`\Longrightarrow \bar x = \displaystyle (3)/(4) \int\limits^4_0 {x[√(x) -(1)/(2)x ]} \, dx\\\\\\\\\Longrightarrow \bar x = \displaystyle (3)/(4)\int\limits^4_0 {[x^{(3)/(2) } -(1)/(2)x^2 ]} \, dx\\\\\\\\\Longrightarrow \bar x = (3)/(4)\Big[(2)/(5)x^{(5)/(2)}- (1)/(6)x^3 \Big]\limits^4_0\\\\\\\\\Longrightarrow \bar x = (3)/(4)\Big(\Big[(2)/(5)(4)^{(5)/(2)}- (1)/(6)(4)^3\Big] -[0]\Big)\\\\\\\\`

`\Longrightarrow \displaystyle \bar x = (3)/(4)\Big[(64)/(5)- (32)/(3)\Big]\\\\\\\\\Longrightarrow \displaystyle \bar x = (3)/(4)\Big[(32)/(15)\Big]\\\\\\\\\therefore \boxed{\bar x =(8)/(5) }`

Now, we need to find the y-coordinate of the centroid:

`\displaystyle \Longrightarrow \bar y = (3)/(4) \int\limits^4_0 {(1)/(2) [(√(x) )^2-((1)/(2)x )^2]} \, dx \\\\\\\\\displaystyle \Longrightarrow \bar y = (3)/(4) \cdot (1)/(2) \int\limits^4_0 { [x-(1)/(4)x^2]} \, dx \\\\\\\\ \Longrightarrow \bar y = (3)/(8) \Big[(1)/(2)x^2 - (1)/(12)x^3 \Big]\limits^4_0\\\\\\\\ \Longrightarrow \bar y = (3)/(8) \Big(\Big[(1)/(2)(4)^2 - (1)/(12)(4)^3\Big] -[0]\Big)\\\\\\\\`

`\displaystyle \Longrightarrow \bar y = (3)/(8) \Big[8 - (16)/(3) \Big]\\\\\\\\\displaystyle \Longrightarrow \bar y = (3)/(8) \Big[(8)/(3) \Big]\\\\\\\\\therefore \boxed{\bar y = 1}`

Thus,

`(\bar x , \bar y)=\boxed{\boxed{\Big((8)/(5), \ 1 \Big)}}`

`\hrulefill`

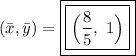
Additional information:

Centroid: The centroid of a 2D shape is the point at which the shape would balance if it were placed on a needle or a pin. For a region bounded by two curves in the Cartesian plane, the centroid is the point that represents the "center of mass" of the region.

Power Rule for Integration: The power rule is a fundamental rule in calculus used to integrate functions of the form x raised to a constant power. The power rule for integration states:


`\boxed{\left\begin{array}{ccc}\text{\underline{Power Rule:}}\\\\\displaystyle\int {x^n} \, dx=(x^(n+1))/(n+1) \end{array}\right }`