Question

The circle below has center O, and its radius is 3 ft. Given that mZAOB-140°, find the area of the shaded region and the length of the arc ADB.

Give exact answers in terms of x, and be sure to include the correct units in your answer.
Area of shaded region:
Length of ADB:

Answer 1

The area of the shaded region is
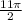`(11\pi)/(2)`, and the length of the arc ADB is
`(11\pi)/(3)`.

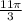Explanation:

Since we wish to find the area of the shaded region, which is a sector of a circle, and the length of an arc, which is part of the circle's circumference, we start off by finding the area of circumference of the circle.

The circle's area can be expressed as
`\pi r^2 = \pi \cdot 3^2 = 9\pi`, and the circumference as
`2\pi r = 2\pi\cdot 3 =6\pi`.

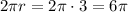Now, since
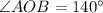`\angle AOB = 140^(\circ)`, we have that reflex angle
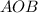`AOB` has measure
`360^(\circ)-140^(\circ)=220^(\circ)`.

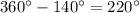Because the length of any arc on the circle or the area of any sector is directly proportional to the measure of the central angle, we have that the area of the shaded sector is
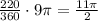`(220)/(360) \cdot 9\pi = (11\pi)/(2)`, and the length of the arc, since arc ADB is the major arc, is
`(220)/(360) \cdot 6\pi = (11\pi)/(3)`.