Answer:
The nth term 77 has n = 17.
Explanation:
My apologies for the solution being in English, as my Spanish is rather poor.
In an arithmetic sequence, the common difference between any two terms is equal. We can then define the first term of the given arithmetic sequence to be
 and the nth term as
and the nth term as
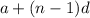 .
.
Since we are given the first and ninth terms, we have:
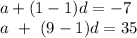
Solving this system, we find that
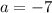 and
and
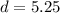 .
.
Now, we need to solve the equation
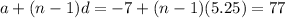 .
.
Adding
 to both sides, dividing by
to both sides, dividing by
 , then adding 1, we find that
, then adding 1, we find that
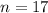 .
.
A much simpler solution is this:
since
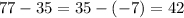 , and the sequence is of an arithmetic nature, then
, and the sequence is of an arithmetic nature, then
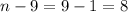 and
and
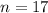 .
.