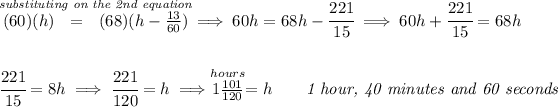Question

A truck enters a highway driving 60 mph. A car enters the highway at the same place 13 minutes later and drives 68 mph in the same direction. From the time the car enters the highway, how long will it take the car to pass the truck?

Answer 1

so let's say the first vehicle, truck A by the time they both meet, namely have covered the same distance "d" miles, truck A has been going already for "h" hours.

Now, enter truck B at 68mph 13 minutes later, well, since an hour has 60 minutes, 13 minutes is really just 13/60 of an hour, and since this truck went in 13 minutes after the first truck A, it has been going for "h" minus 13 minutes or "h" minus 13/60 hours, so

`{\Large \begin{array}{llll} \underset{distance}{d}=\underset{rate}{r} \stackrel{time}{t} \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{lcccl} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ A&d&60&h\\ B&d&68&h-(13)/(60) \end{array}\hspace{5em} \begin{cases} d=(60)(h)\\\\ d=(68)(h-(13)/(60)) \end{cases} \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{substituting on the 2nd equation}}{(60)(h)~~ = ~~(68)(h-(13)/(60))}\implies 60h=68h-\cfrac{221}{15}\implies 60h+\cfrac{221}{15}=68h \\\\\\ \cfrac{221}{15}=8h \implies \cfrac{221}{120}=h\implies \stackrel{ hours }{1(101)/(120)}=h\qquad \textit{1 hour, 40 minutes and 60 seconds}`