Question

Suppose that prices of a gallon of milk at various stores in one town have a mean of $3.91 with a standard deviation of $0.13. Using Chebyshev's Theorem, what is the minimum percentage of stores that sell a gallon of milk for between $3.65 and $4.17

Answer 1

The minimum percentage of stores that sell a gallon of milk for between $3.65 and $4.17 is of 75%.

Explanation:

Chebyshev Theorem

The Chebyshev Theorem can also be applied to non-normal distribution. It states that:

At least 75% of the measures are within 2 standard deviations of the mean.

At least 89% of the measures are within 3 standard deviations of the mean.

An in general terms, the percentage of measures within k standard deviations of the mean is given by
`100(1 - (1)/(k^(2)))`.

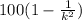In this question:

We have a mean of $3.91 and a standard deviation of $0.13.

Using Chebyshev's Theorem, what is the minimum percentage of stores that sell a gallon of milk for between $3.65 and $4.17?

3.65 = 3.91 - 2*0.13

4.17 = 3.91 + 2*0.13

Within 2 standard deviations of the mean, so, by the Chebyshev's Theorem, the minimum percentage of stores that sell a gallon of milk for between $3.65 and $4.17 is of 75%.