Formulate an expression for the surface energies of ideal (100),(110), and (111) surfaces of a material that adopts a simple cubic crystal structure. Leave your expression for γ in terms of a and ΔHsub. .
the calculation step by step.
Given:
1. F_C: The force applied vertically downward at point C = 100 lbs
2. BD: The length of link BD = 6 inches
3. a: The horizontal distance from A to the line of action of force F_C = 4 inches
4. θ: The angle that link AB makes with the horizontal = 15° (this will be used to calculate the horizontal distance that force F_C acts from point B)
Here is how we would set up the problem:
Step 1: Identify the System and Assumptions
- The system is in static equilibrium, which means the sum of the forces and moments in any direction equals zero.
- We assume all joints are pin joints, and the weight of the links can be neglected.
Step 2: Define the Equilibrium Equations
For static equilibrium of a body, the sum of the moments about any point is zero. We will calculate moments about point B because it eliminates the need to consider forces at point B (since their moment arm would be zero).
Step 3: Calculate the Moment Arm for F_C
Since AB is at an angle of 15°, we will calculate the horizontal distance from B to where F_C is applied using the length of BD and the angle θ:
![\[ \text{Horizontal distance} = a + (\text{BD} * \cos(θ)) \]](https://img.qammunity.org/2024/formulas/engineering/college/j24rhg2jaypqi67llkyv3mnzul1so8099r.png)
Now, plugging in the numbers:
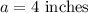
![\[ \text{BD} = 6 \text{ inches} \]](https://img.qammunity.org/2024/formulas/engineering/college/2jqxfbheqp75vz6a2lxmjqehg7z61q05du.png)
![\[ θ = 15° \]](https://img.qammunity.org/2024/formulas/engineering/college/u9ip3mdsxwgdr9iz564gu51uoht0fyd8uu.png)
![\[ \cos(θ) = \cos(15°) \]](https://img.qammunity.org/2024/formulas/engineering/college/ivs9o3238ryz6q3w05z60q8son4fu4str1.png)
Step 4: Moment Equation about Point B
Set up the moment equation about point B where clockwise moments are set to equal counter-clockwise moments. The force at C creates a clockwise moment, and the horizontal force exerted on E creates a counter-clockwise moment.
![\[ F_C * (\text{Horizontal distance}) = F_E * (\text{BD}) \]](https://img.qammunity.org/2024/formulas/engineering/college/nvva1s6lwq4p853cg0iq44yiukpau3hiir.png)
Step 5: Solve for F_E
Now, we will substitute the values and solve for F_E:
![\[ 100 * (4 + 6 * \cos(15°)) = F_E * 6 \]](https://img.qammunity.org/2024/formulas/engineering/college/s3ylm11si9ttdsomnpbugycew318pwrlwy.png)
Step 6: Calculate F_E
![\[ F_E = (100 * (4 + 6 * \cos(15°)))/(6) \]](https://img.qammunity.org/2024/formulas/engineering/college/99bqteny8rvbn16ddo0tjxh3bl0ukl8bxp.png)
Step 7: Numerical Substitution and Computation
Now let's do the numerical substitution and computation:
![\[ \cos(15°) \approx 0.9659 \]](https://img.qammunity.org/2024/formulas/engineering/college/855wvzlg4w8l2b6grjl8maqgw5ujaibdo9.png)
S
![\[ F_E = (100 * (4 + 6 * 0.9659))/(6) \]](https://img.qammunity.org/2024/formulas/engineering/college/wjlr68dnr7z31dq9ubg56o3o7mao0pcqdo.png)
![\[ F_E \approx (100 * (4 + 5.7954))/(6) \]](https://img.qammunity.org/2024/formulas/engineering/college/a624xuj16yqv9mtcbdfy5msozx2l7vxnkd.png)
![\[ F_E \approx (100 * 9.7954)/(6) \]](https://img.qammunity.org/2024/formulas/engineering/college/bxpvfvcbnoo39dk0er06pyo8e3jn5s243a.png)
![\[ F_E \approx (979.54)/(6) \]](https://img.qammunity.org/2024/formulas/engineering/college/k0y3wbfqql3imbtbfmm09fjj1mtiga0k7p.png)
![\[ F_E \approx 163.26 \text{ lbs} \]](https://img.qammunity.org/2024/formulas/engineering/college/hdsz0ajuhx1kflijwy8b5lm2y6nfuu23x7.png)
Thus, the horizontal force exerted on block E is approximately 163.26 lbs.
The diagram of the question given below: