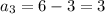Question

Find the general term for the following sequence:
5, 4, 3, 2

Answer 1

`\textsf{Recursive\;de\:\!finition:}\quad &a_n&=a_(n-1)-1,\;\;\textsf{with}\;a_0=5`

`\textsf{Closed\;formula:}\quad &a_n&=5-n,\quad \textsf{where\;$a_0$\;is\;the\;first\;term}`

`\textsf{$\sf n^(th)$\;term\;formula:}\quad &a_n&=6-n,\quad \textsf{where\;$a_1$\;is\;the\;first\;term}`

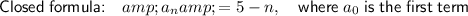
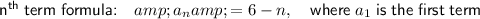
Explanation:

Given sequence:

• 5, 4, 3, 2, ...

The given sequence is arithmetic, as there is a common difference between consecutive terms. (Each term is 1 less than the previous term).

If the initial term (a₀) of the sequence is a, and the common difference is d, then:

`\large\boxed{\begin{aligned}\phantom{w}\\&\textsf{Recursive\;de\:\!finition:}\quad &a_n&=a_(n-1)+d,\;\;\textsf{with}\;a_0=a\\\\&\textsf{Closed\;formula:}\quad &a_n&=a+dn\\\phantom{w}\end{aligned}}`

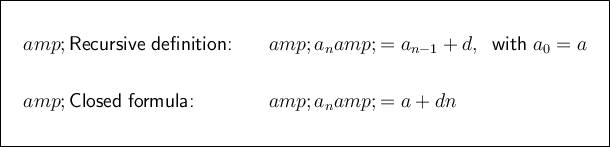
To find the common difference (d), subtract a term from the following term:

`d = 4-5=-1`

`d=3-4=-1`

`d=2-3=-1`

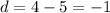
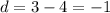
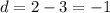
Therefore, the common difference of the given sequence is d = -1.

The first term is 5. Therefore, a₀ = 5.

Plug the values of d and a₀ into the recursive definition:

`\textsf{$a_n=a_(n-1)-1$\quad with\;\;$a_0=5$}`

For the closed formula, as a₀ = a, then a = 5.

Therefore, plug the values of d and a into the closed formula:

`a_n=a+dn`

`a_n=5+(-1)n`

`a_n=5-n`

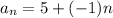
Therefore, for the given arithmetic sequence, the recursive definition and the closed formula are:

`\large\boxed{\begin{aligned}\phantom{w}\\&\textsf{Recursive\;de\:\!finition:}\quad &a_n&=a_(n-1)-1,\;\;\textsf{with}\;a_0=5\\\\&\textsf{Closed\;formula:}\quad &a_n&=5-n\\\phantom{w}\end{aligned}}`

`\hrulefill`

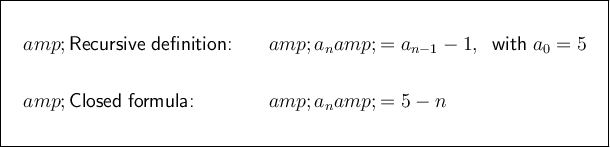
The general formula to find the nth term of an arithmetic sequence is:

`\large\boxed{a_n=a_1+(n-1)d}`

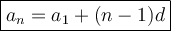
where:

• aₙ is the nth term of the arithmetic sequence.
• a₁ is the first term of the sequence.
• d is the common difference between consecutive terms.
• n is the position of the term.

For the given sequence 5, 4, 3, 2, ..., the first term is 5 and the common difference is -1.

Therefore, substitute a₁ = 5 and d = -1 into the general formula:

`a_n=5+(n-1)(-1)`

`a_n=5-n+1`

`a_n=6-n`

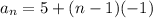
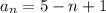
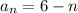
Therefore, the equation to find the nth term for the given arithmetic sequence is:

`\large\boxed{a_n=6-n}`

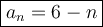
where n is the position of the term.

For example, to find the 3rd term, we substitute n = 3 into the nth term equation:

`a_3=6-3=3`