Question

Find the equation of the line parallel to y = -2x + 2 which passes through (0,-1)​

Answer 1

Equation of parallel line is y = -2x - 1

Explanation:

The given line
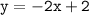`\tt y = -2x + 2` is in slope-intercept form
`\boxed{\tt y = mx + b}`, where "m" is the slope.

In this case, the slope of the given line (m)= -2.

Now, for the parallel line, it has the same slope as the given line (parallel lines have the same slope).

So, the slope "m" of the new line is also -2.

Now, we have the slope (-2) and a point (0, -1) through which the new line passes.

We can use the point-slope form of a line to find the equation:

Point-slope form:

`\boxed{\tt y - y_1 = m(x - x_1)}`

where (x1, y1) is the given point and "m" is the slope.

Plugging in the values: (x1, y1) = (0, -1) and m = -2:

y - (-1) = -2(x - 0)

y + 1 = -2x

Now, we can rewrite it in slope-intercept form (y = mx + b):

y = -2x - 1

So, the equation of the line parallel to y = -2x + 2 and passing through the point (0, -1) is y = -2x - 1.