Answer:
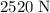 downwards (assuming that the weight of the bungee cord is negligible.)
downwards (assuming that the weight of the bungee cord is negligible.)
Step-by-step explanation:
To find the magnitude of the unknown force, start by considering all the forces acting on this person. Assuming that this person isn't moving, derive an equation from the fact that the resultant force on this person should be zero. Solve this equation to obtain the magnitude and orientation (upward or downward) of the unknown force.
Under the assumptions, forces on this person include:
- Restoring force from the bungee cord (upward,)
- Weight of the person (downward,) and
- Unknown force on the person.
With a spring constant of
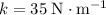 at
at
 from the equilibrium position, the restoring force from the bungee cord would be:
from the equilibrium position, the restoring force from the bungee cord would be:
 .
.
Given that
 , weight of the person would be:
, weight of the person would be:
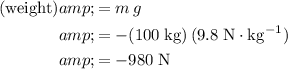 .
.
(Note that since weight points downwards, the sign in front of this force should be negative.)
Assuming that this person is stationary (acceleration is zero,) the resultant force on this person should be zero. In other words:
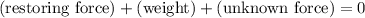 .
.
Rearrange this equation and solve for the unknown force:
 .
.
(Note that the sign in front of this unknown force is negative since this force is supposed to point downwards.)
In other words, a force of magnitude
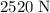 pointing downwards is required.
pointing downwards is required.