Question

What is the concentration of H^+ions at pH =6

Answer 1

Answer: What is the concentration of H+ ions at a pH = 2?

⇒ 0.01 mol/L

What is the concentration of H+ ions at a pH = 6?

⇒ 0.000001 mol/L

How many more H+ ions are there in a solution at a

pH = 2 than in a solution at a pH = 6?

⇒ 10,000

Explanation: I hope this helps

Answer 2

Concentration of H+ ions at pH = 2=
`\boxed{0.01}`

Concentration of H+ ions at pH = 6=
`\boxed{0.000001}`

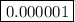
There are
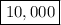`\boxed{10,000}` times more H+ ions in a solution at pH =2 and PH=6.

Step-by-step explanation:

The pH of a solution is defined as:

`\boxed{\tt pH = -log[H^+]}}`

where [H+] represents the concentration of H+ ions in mol/L.

In order to calculate the concentration of H+ ions at a given pH, we rearrange the formula:

`\boxed{\tt [H^+] = 10^(-pH)}`

Now, let's calculate the concentration of H+ ions at pH = 2 and pH = 6:

1. Concentration of H+ ions at pH = 2:

`\tt [H^+] (pH = 2) = 10^(-2) \textsf{mol/L}`

2. Concentration of H+ ions at pH = 6:

`\tt [H^+] (pH = 6) = 10^(-6) \textsf{ mol/L}`

Now, to find how many more H+ ions there are in a solution at pH = 2 than in a solution at pH = 6, divide the concentration at pH = 2 by the concentration at pH = 6:

`\tt ([H^+] (pH = 2) )/( [H^+] (pH = 6) )= ((10^(-2) mol/L) )/((10^(-6) mol/L) )\\\\= 10^(-2 - (-6)) = 10^(-2 + 6)= 10^4`

So, there are 10,000 times more H+ ions in a solution at pH = 2 than in a solution at pH = 6.