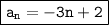Question

PLEASE HELP ASAP
Find the general term definition for the sequence
-1, -4, -7, -10

Answer 1

-3n+2

Explanation:

Here, the sequence is -1, -4, -7, -10

First term (a) = -1

common difference (d) = t2-t1 = -4-(-1) = -3

the general term tn= a+(n-1)d

= -1+(n-1)-3

= -1-3n+3

= -3n+2

Answer 2

`\boxed{\tt a_n = -3n + 2}`

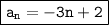
Explanation:

The sequence -1, -4, -7, -10 is an arithmetic sequence.

In an arithmetic sequence, each term is found by adding a constant value to the preceding term.

In this case, the constant value or common difference is -4-(-1)=-3

The general term definition for an arithmetic sequence is:

`\boxed{\tt a_n = a_1 + d(n - 1)}`

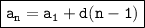
where:

• 
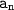  `\tt a_n` is the nth term in the sequence
• 
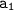  `\tt a_1` is the first term in the sequence
• d is the common difference

In this case, the first term is
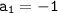`\tt a_1 = -1` and the common difference is d = -3. So, the general term definition for the sequence -1, -4, -7, -10 is:

`\tt a_n = -1 - 3(n - 1) = -3n + 2`

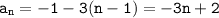
This means that the nth term in the sequence or General Term is :
`\boxed{\tt a_n = -3n + 2}`