Question

Suppose that the monthly cost of a long-distance phone plan (in dollars) is a linear function of the total calling time (in minutes). When graphed, the function

gives a line with a slope of 0.13. See the figure below.
The monthly cost for 55 minutes of calls is $17.82. What is the monthly cost for 52 minutes of calls?

Answer 1

$17.52

Explanation:

As we have been given the slope of the line, m = 0.13, and a point on the line (55, 17.82), we can input these into the point-slope form of a linear equation to create an equation of the line.

`\begin{aligned}y-y_1&=m(x-x_1)\\y-17.82&=0.13(x-55)\\y-17.82&=0.13x-7.15\\y&=0.13x+10.67\end{aligned}`

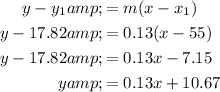
Therefore, the equation of the line is:

`\large{\boxed{y=0.13x+10.67}`

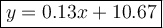
where:

• x is the total calling time (in minutes).
• y is the monthly plan cost (in dollars).

Now we have an equation for the line, to determine the monthly cost for 52 minutes of calls, substitute x = 52 into the equation and solve for y:

`\begin{aligned}x=52 \implies y&=0.13(52)+10.67\\y&=6.76+10.67\\y&=17.43\end{aligned}`

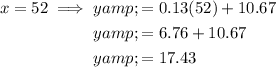
Therefore, the monthly cost for 52 minutes of calls is $17.43.