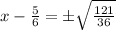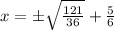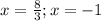Question

3a^2-5a-8=0 solve by completing the square

Answer 1

`x=(8)/(3);x=-1`

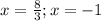
Explanation:

ax² + bx + c = 0 | use the equation for complete the square

x² + (
`(b)/(a)`)x +
`(c)/(a)` = 0

x² + (
`(b)/(a)`)x = -
`(c)/(a)`

x² + (
`(b)/(a)`)x + (
`(b)/(2a)`)² = (
`(b)/(2a)`)² -
`(c)/(a)`

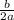`(x+(b)/(2a))^(2) = (b^(2)-4ac)/(4a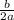^(2))`

let the equation 3a² - 5a - 8 = 0 be 3x² - 5a - 8, where using the above equation, a = 3, b = -5, c = -8

plugging into the equation we get:

`(x+(-5)/(2(3)))^(2) = ((-5)^(2)-4(3)(-8))/(4(3)^(2))`

`(x + (-5)/(6))^(2) = (25+96)/(36)`

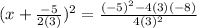
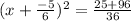
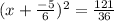`(x + (-5)/(6))^(2) = (121)/(36)` | isolate x

`x - (5)/(6) = \pm\sqrt{(121)/(36)}`

`x = \pm\sqrt{(121)/(36)}+(5)/(6)`

`x=\pm(11)/(6)+(5)/(6)`

`x=(8)/(3);x=-1`

Answer 2

First, let's move the constant term to the right side of the equation:

3a^2 - 5a = 8

Next, we need to divide both sides by the coefficient of the squared term, which is 3:

a^2 - (5/3)a = 8/3

To complete the square, we need to add and subtract the square of half of the coefficient of the linear term, which is (5/6)^2:

a^2 - (5/3)a + (5/6)^2 - (5/6)^2 = 8/3

The left side is now a perfect square:

(a - 5/6)^2 = 8/3 + 25/36

Combining the fractions on the right side:

(a - 5/6)^2 = (64/36) / (3/3)

(a - 5/6)^2 = 64/108

(a - 5/6)^2 = 16/27

Taking the square root of both sides:

a - 5/6 = ± √(16/27)

a - 5/6 = ± 4/3√3

Adding 5/6 to both sides:

a = 5/6 ± 4/3√3

Therefore, the solutions to the equation are:

a = 5/6 + 4/3√3 or a = 5/6 - 4/3√3.