Question

Can someone send the answers please

Answer 1

1. To classify quadrilateral

A quadrilateral is a polygon with four sides. There are many different ways to classify quadrilaterals, but some of the most common classifications include:

• Convex quadrilateral: A quadrilateral with all four interior angles less than 180 degrees.
• Concave quadrilateral: A quadrilateral with at least one interior angle greater than 180 degrees.
• Trapezoid: A quadrilateral with one set of parallel sides.
• Parallelogram: A quadrilateral with two sets of parallel sides.
• Rectangle: A parallelogram with four right angles.
• Square: A rectangle with all four sides of equal length.

`\hrulefill`

2. To classify the triangle

A triangle is a polygon with three sides. There are many different ways to classify triangles, but some of the most common classifications include:

• Equilateral triangle: A triangle with all three sides of equal length.
• Isosceles triangle: A triangle with two sides of equal length.
• Scalene triangle: A triangle with no sides of equal length.
• Right triangle: A triangle with a right angle (90 degrees).

`\hrulefill`

3. Use the distance formula:

The distance formula is used to find the distance between two points in a coordinate plane. The formula is:

`\boxed{\tt d = √((x_2- x_1)^2 + (y_2 - y_1)^2)}`

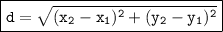
where dis the distance between the two points, x1 and x2 are the x-coordinates of the two points, and y1 and y2 are the y-coordinates of the two points.

`\hrulefill`

4. Use the midpoint formula

The midpoint formula is used to find the midpoint of a segment. The formula is:

`\boxed{\tt m(x,y) =( ((x1 + x2) )/(2), ((y1 + y2) )/( 2))}`

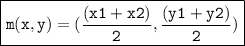
where m(x,y) is midpoint and (x1, y1) and (x2, y2) are the endpoints of the segment.

What can I find with midpoint formula?

The midpoint formula can be used to find the midpoint of a segment, which is the point that is exactly halfway between the two endpoints of the segment. The midpoint formula can also be used to find the coordinates of a point that is a certain distance away from two other points.

`\hrulefill`

5. Slope

The slope is a measure of the steepness of a line. It is calculated by dividing the change in the y-coordinate (rise) by the change in the x-coordinate (run). The slope of a line can be positive, negative, zero, or undefined.

• To find it from a graph

The slope of a line can be found from a graph by drawing a line segment from the point where the line crosses the y-axis to the point where the line crosses the x-axis. The slope of the line is equal to the rise over run of the line segment.

• To find it from two points

The slope of a line can also be found from two points by using the following formula:

`\boxed{ \tt m =( (y_2 - y_1) )/( (x2 - x1))}`

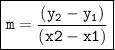
where m is the slope of the line, y2 and y1 are the y-coordinates of the two points, and x2 and x1 are the x-coordinates of the two points.