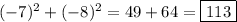Find the sum of the squares of two consecutive negative integers that equal 113

Question

asked Jan 18, 2024 189k views

1 Answer

James Skimming · Answer 1 · 2024-01-23T23:05:00+0000

Answer:

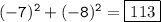
$\tt (-7)^2 + (-8)^2 = \boxed{113}$

Explanation:

Let's call the two consecutive negative integers x and x - 1.

We know that the sum of their squares is equal to 113, so we have the equation:

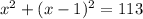
x^2 + (x - 1)^2 = 113

Expanding the squares on the left-hand side, we get:

x^2 + x^2 - 2x + 1 = 113

Combining like terms, we get:

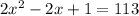
2x^2 - 2x + 1 = 113

Subtracting 1 and 2x from both sides, we get:

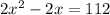
2x^2 - 2x = 112

Dividing both sides by 2, we get:

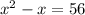
x^2 - x = 56

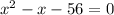
x^2 - x -56=0

Factoring the left-hand side, we get:

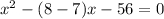
x^2-(8-7)x-56 =0

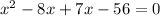
x^2 -8x +7x -56 =0

x(x-8) +7(x-8)=0

(x-8)(x+7)=0

Setting each factor equal to 0, we get:

$x - 8 = 0 \text{ or } x + 7 = 0$

Solving for x we get:

$x = 8 \text{ or } x = -7$

Since x is negative, the only solution that works is x = -7.

Here 8 is positive while squaring we get 64 for (-8) too.

So, another negative integer is -8.

Therefore, the two consecutive negative integers that add up to 113 are -7 and -8. The sum of their squares is:

$(-7)^2 + (-8)^2 = 49 + 64 = \boxed{113}$