Question

EMERGENCY! Please explain your answer in steps, and don't forget to round, thank you.

Answer 1

`P \approx \$ 75.64`

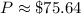
Explanation:

To determine the amount the Turner family needs to pay into the annuity each month, we can use the formula for the future value of an ordinary annuity:

`\rightarrow FV = P ((1 + i)^n - 1)/(i)`

Where:

• FV = Future value of the annuity ($12,000 in this case)

• P = Payment at end of each period (unknown)

• i = Monthly interest rate (5.4% divided by 12, or 0.054/12)

• n = Number of compounding periods (10 years multiplied by 12 months, or 10 · 12)

Substituting the known values into the formula, we can solve for P:

`\Longrightarrow 12000 = P ((1 + (0.054)/(12))^(10 \cdot 12) - 1)/((0.054)/(12))`

Now, let's calculate it:

`\Longrightarrow 12000 = P ((1 + 0.0045)^(120) - 1)/(0.0045)\\\\\\\\\Longrightarrow P = (12000) (0.0045)/((1 + 0.0045)^(120) - 1)\\\\\\\\ \Longrightarrow P = (54)/((1.0045)^(120) - 1)\\\\\\\\\Longrightarrow P = (54)/(0.713929)`

Using a calculator, we find:

`\therefore \boxed{\boxed{P \approx \$ 75.64}}`

Therefore, the Turner family needs to pay approximately $75.64 into the annuity each month in order to have a total value of $12,000 after 10 years.