Question

I cannot figure this one out.

Answer 1

`\textsf{A.} \ \, x\approx -0.75 \: \textsf{ and } \: x\approx 5.5`

Explanation:

We need to approximate the x-values that satisfy the equation. In other words, we need to find the x-values that make the equation true.

We can see that two functions have been graphed on the coordinate plane:

• in blue:
  `y = 2\, |x - 2| - 5`
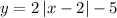
• in red:
  `y = √(x + 3) - 1`

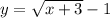
We can also see that these are both sides of the given equation:

`2\,|x-2| -5 =√(x+3)-1`

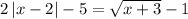
Therefore, the x-values that will satisfy the equation are the ones where the red and blue functions have the same output — where they cross on the graph.

We can identify these x-values as approximately:
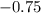`-0.75` and
`5.5`. So, the correct answer is:

`\textsf{A.} \ \, x\approx -0.75 \: \textsf{ and } \: x\approx 5.5`