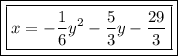Question

Write the equation for a parabola with a focus at (-7.-5) and a directrix at

x=−4

x=?

Answer 1

Check the picture below.

so the parabola looks more or less like so, since the vertex is half-way between the focus point and directrix, that puts it there, with a "p" distance of 1.5 and since it opens to the left, is negative, so

`\textit{horizontal parabola vertex form with focus point distance} \\\\ 4p(x- h)=(y- k)^2 \qquad \begin{cases} \stackrel{vertex}{(h,k)}\qquad \stackrel{focus~point}{(h+p,k)}\qquad \stackrel{directrix}{x=h-p}\\\\ p=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix}\\\\ \stackrel{p~is~negative}{op ens~\supset}\qquad \stackrel{p~is~positive}{op ens~\subset} \end{cases} \\\\[-0.35em] ~\dotfill`

`\begin{cases} h=-5.5\\ k=-5\\ p=-1.5 \end{cases}\implies 4(-1.5)(~~x-(-5.5)~~) = (~~y-(-5)~~)^2 \\\\\\ -6(x+5.5)=(y+5)^2\implies x+5.5=-\cfrac{1}{6}(y+5)^2 \\\\\\ ~\hfill~ {\Large \begin{array}{llll} x=-\cfrac{1}{6}(y+5)^2-5.5 \end{array}}~\hfill~`

Answer 2

`\textsf{Standard form:} \quad (y+5)^2=-6(x+5.5)`

`\textsf{Vertex form:} \quad x=-(1)/(6)(y+5)^2-5.5`

`\textsf{Expanded form:} \quad x=-(1)/(6)y^2-(5)/(3)y-(29)/(3)`

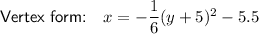
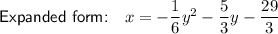
Explanation:

The directrix of a parabola is a fixed line outside of the parabola that is perpendicular to the axis of symmetry. As the given directrix of the parabola is the vertical line x = -4, this means the axis of symmetry is horizontal.

The standard form of a parabola with a horizontal axis of symmetry is:

`\large\boxed{(y-k)^2=4p(x-h)}`

where

• p ≠ 0
• Vertex = (h, k)
• Focus = (h+p, k)
• Directrix: x = (h - p)
• Axis of symmetry: y = k

Given the focus is (-7, -5):

• 
  `h + p = -7`
• 
  `k = -5`

Given the directrix is x = -4:

• 
  `h - p = -4`

The x-value of the vertex (h) is the midpoint between the x-values of the focus and the directrix. Therefore:

`h=(-7-4)/(2)=-5.5`

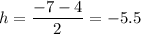
To find the value of p, substitute the found value of h into the formula for the directrix:

`-5.5-p=-4`

`-5.5+4=p`

`p=-1.5`

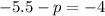
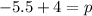
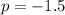
Substitute the values of h, k and p into the standard formula:

`(y-(-5))^2=4(-1.5)(x-(-5.5))`

`(y+5)^2=-6(x+5.5)`

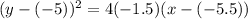
Therefore, the equation of the parabola in standard form is:

`\boxed{\boxed{(y+5)^2=-6(x+5.5)}}`

To write the equation vertex form, divide both sides by -6:

`-(1)/(6)(y+5)^2=x+5.5`

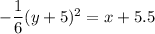
Subtract 5.5 from both sides of the equation:

`x=-(1)/(6)(y+5)^2-5.5`

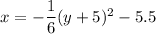
Therefore, the equation of the parabola in vertex form is:

`\boxed{\boxed{x=-(1)/(6)(y+5)^2-5.5}}`

To write the equation expanded form, expand the brackets:

`x=-(1)/(6)(y^2+10y+25)-5.5`

`x=-(1)/(6)y^2-(10)/(6)y-(25)/(6)-5.5`

`x=-(1)/(6)y^2-(5)/(3)y-(29)/(3)`

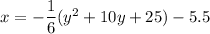
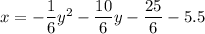
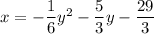
Therefore, the equation for the parabola in expanded form is:

`\boxed{\boxed{x=-(1)/(6)y^2-(5)/(3)y-(29)/(3)}}`