Question

= P12 Q.30. A motor is lifting a mass of 35 kg at a constant speed of 6.0 m/s. If friction is neglected, the power developed by the motor to do this lifting is 5.8 W 57 W 210 W 2.1 kW 1.5 kW A) B) C) (D) E​

Answer 1

Approximately
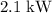`2.1\; {\rm kW}`. (Assuming that
`g = 9.81\; {\rm N \cdot kg^(-1)}`.)

Step-by-step explanation:

The question is asking for the power output of this motor. Power is the rate at which work is being done.

To find the power of this motor, start by finding the force that the motor is exerting. Based on the speed of the motion of the motor, find the amount of work completed in a given amount of time. Finally, divide the amount of work completed by the duration to find the power of the motor.

In this question, the weight of this
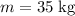`m = 35\; {\rm kg}` mass is:

`\begin{aligned}m\, g &= (35\; {\rm kg})\, (9.81\; {\rm N\cdot kg^(-1)}) \\ &= 343.35\; {\rm N}\end{aligned}`.

Assuming that friction and the weight of the cable are negligible, the force that this motor exerts would be equal to the weight of the mass:
`343.35\; {\rm N}`.

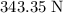It is given that the motor lifts the mass at a speed of
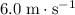`6.0\; {\rm m\cdot s^(-1)}`. In other words, the motor lifts the mass by
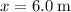`x = 6.0\; {\rm m}` over the duration of
`t = 1\; {\rm s}`.

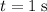Multiply the force the motor exerted (
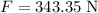`F = 343.35\; {\rm N}`) by the displacement in the direction of the force (
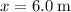`x = 6.0\; {\rm m}`) to find the amount of work completed:

`W = F\, t = (343.35\; {\rm N})\, (6.0\; {\rm m}) \approx 2.1* 10^(3)\; {\rm J}`.

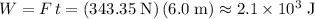(Note that
`1\; {\rm N\cdot m} = 1\; {\rm J}`.)

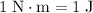Divide the amount of work completed
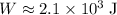`W \approx 2.1 * 10^(3)\; {\rm J}` by the duration
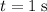`t = 1\; {\rm s}` over which the work was done to find the power:

`\begin{aligned}P &= (W)/(t) \\ &= \frac{2.1* 10^(3)\; {\rm J}}{1\; {\rm s}} \\ &= 2.1* 10^(3)\; {\rm W}\end{aligned}`.

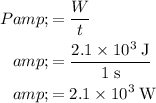(Note that
`1\; {\rm J \cdot s^(-1)} = 1\; {\rm W}`.)

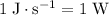In general, power
`P` can be found directly from force
`F` and velocity
`v` in the direction of the force using the equation
`P = F\, v`.