Question

What is the answer to the question?

Answer 1

Answer: x=3

Explanation:

To solve the question 2ln
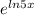`e^(ln5x)` = 2ln15, first you have to simplify the equation. e cancels out ln (and vice versa), so on the left side of the equation, first simplify it to 2ln(5x).

The 5x comes down from the exponent once the e cancels out the ln.

Next divide both sides by 2. That will leave you with ln(5x) = 2ln(15)

Raise both sides by the power of e. It should look like this:

`e^(ln5x) =e^{ln15`

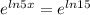
As said before, e cancels out ln. When this action is done, the numbers/variables left as the exponent become bases.

You should be left with 5x=15.

Divide both sides by 5 to find that the answer is x=3.

The picture attached gives a clearer step-by-step explanation.

Answer 2

2 * In(e^n * 5x) = 2 * In(15) is x = 3 / e^n.

Explanation:

To find the true solution to the equation 2 * In(e^n * 5x) = 2 * In(15), where n is a constant, we can simplify the equation using the properties of logarithms.

First, let's rewrite the equation using the fact that ln(e) = 1:

2 * In(e^n * 5x) = 2 * In(15)

In(e^n * 5x) = In(15)

e^n * 5x = 15

Next, let's isolate the variable x:

e^n * 5x = 15

5x = 15 / e^n

x = (15 / e^n) / 5

x = 15 / (5 * e^n)

x = 3 / e^n

Therefore, the true solution to the equation 2 * In(e^n * 5x) = 2 * In(15) is x = 3 / e^n.