Question

Simplify the square root of 20^8

Answer 1

160,000

Explanation:

To simplify
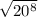`√(20^8)`, we can break down the expression into smaller parts.

First, let's simplify 20⁸. To do that, we can rewrite it as (4 · 5)⁸.

Now, using the properties of exponents, we can expand the expression as follows:

⇒ (4 · 5)⁸ = 4⁸ · 5⁸

The next step is to simplify the individual exponents:

⇒ 4⁸ = (2²)⁸ = 2²⁽⁸⁾ = 2¹⁶

⇒ 5⁸ = 5²⁽⁴⁾ = (5²)⁴ = 25⁴

Now we can rewrite the expression with the simplified exponents:

⇒ (4 · 5)⁸ = 2¹⁶ · 25⁴

Next, let's simplify the square root of the expression. We can rewrite it as:

√(2¹⁶ · 25⁴) = √2¹⁶ · √25⁴

• The square root of 2¹⁶ is equal to 2^(16/2) = 2⁸ = 256

• The square root of 25⁴ is equal to 25^(4/2) = 25² = 625

Now we can combine the simplified parts:

⇒ √(2¹⁶ · 25⁴) = √2¹⁶ · √25⁴ = 256 · 625 = 160,000

Therefore,
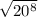`√(20^8)` simplifies to 160,000.