Answer:
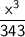
Explanation:
The question is asking us to solve:
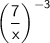
So the entire fraction is raised to the power of -3.
To simplify further, we recall the following exponent law:
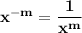
So we flop the number over, like this:
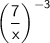
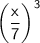
If we have a fraction raised to a power, then both the numerator and the denominator is raised to that power:
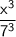
Simplify:
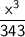
Therefore, the answer is x³/343.