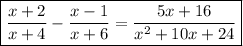Question

Combine as indicated by the signs.
X+ 2
X-1
X+4 X+6

Answer 1

11x + 8

Explanation:

(x+2) (x+6) - (x+4) (x-1)

x^2 + 8x +12 - x^2 + 3x -4

x^2 - x^2 + 8x+3x + 12 -4

= 11x + 8

Answer 2

`(x+2)/(x+4)-(x-1)/(x+6)=(5x+16)/((x+4)(x+6))`

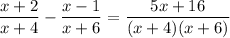
Explanation:

Given expression:

`(x+2)/(x+4)-(x-1)/(x+6)`

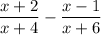
To subtract the fractions we need to make the denominators the same.

The greatest common multiple of the two denominators is (x + 4)(x + 6). Therefore multiply the numerator and denominator of the first fraction by (x + 6), and multiply the numerator and denominator of the second fraction by (x + 4):

`=((x+2)(x+6))/((x+4)(x+6))-((x-1)(x+4))/((x+6)(x+4))`

`=((x+2)(x+6))/((x+4)(x+6))-((x-1)(x+4))/((x+4)(x+6))`

`\textsf{Apply the fraction rule:} \quad (a)/(c)-(b)/(c)=(a-b)/(c)`

`=((x+2)(x+6)-(x-1)(x+4))/((x+4)(x+6))`

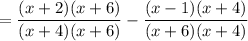
Expand the brackets in the numerator:

`=((x^2+8x+12)-(x^2+3x-4))/((x+4)(x+6))`

`=(x^2+8x+12-x^2-3x+4)/((x+4)(x+6))`

`=(5x+16)/((x+4)(x+6))`

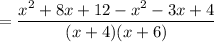
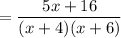
Therefore:

`\boxed{(x+2)/(x+4)-(x-1)/(x+6)=(5x+16)/((x+4)(x+6))}`

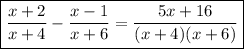
Additional information

If the denominator needs to be expanded too, then:

`\boxed{(x+2)/(x+4)-(x-1)/(x+6)=(5x+16)/(x^2+10x+24)}`