Question

A sample of bacteria is decaying according to a half-life model. If the sample begins with 900 bacteria, and after 15 minutes there are 270 bacteria, after how many minutes will there be 20 bacteria remaining? When solving this problem, round the value of k to four decimal places and round your final answer to the nearest whole number.

Answer 1

47 minutes

Explanation:

As we have not been given the specific half-life of the bacteria, we can use this half-life formula for the given problem:

Half-life formula

`\boxed{N(t)=N_0e^(kt)}`

where:

• N(t) is the quantity remaining.
• N₀ is the initial quantity.
• t is the time elapsed.
• k is the decay constant.

As the initial quantity of bacteria is 900, substitute N₀ = 900 into the formula:

`N(t)=900e^(kt)`

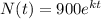
We are told that after 15 minutes there are 270 bacteria. Therefore, to find the value of k, substitute t = 15 and N(t) = 270 into the equation and solve for k (to 4 decimal places):

`\begin{aligned}270&=900e^(15k)\\\\(270)/(900)&=e^(15k)\\\\0.3&=e^(15k)\\\\\ln(0.3)&=\ln\left(e^(15k)\right)\\\\\ln(0.3)&=15k\ln\left(e\right)\\\\\ln(0.3)&=15k\\\\k&=(1)/(15)\ln(0.3)\\\\k&=-0.0802648536...\\\\k&=-0.0803\; \sf (4\;d.p.)\end{aligned}`

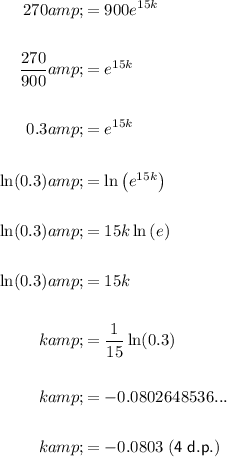
Therefore, the equation that models the given scenario is:

`\large\boxed{N(t)=900e^(-0.0803t)}`

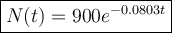
where N(t) is the number of bacteria remaining, and t is the time in minutes.

To calculate after how many minutes there will be 20 bacteria remaining, substitute N(t) = 20 into the equation and solve for t:

`\begin{aligned}20&=900e^(-0.0803t)\\\\(20)/(900)&=e^(-0.0803t)\\\\(1)/(45)&=e^(-0.0803t)\\\\\ln\left((1)/(45)\right)&=\ln \left(e^(-0.0803t)\right)\\\\\ln (1)-\ln(45)&=-0.0803t\ln \left(e\right)\\\\-\ln(45)&=-0.0803t\\\\t&=(-\ln(45))/(-0.0803)\\\\t&=47.4055104...\\\\t&=47\; \sf minutes\;(nearest\;whole\;number)\end{aligned}`

Therefore, there will be 20 bacteria remaining after approximately 47 minutes.