Answer:
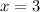 or
or

Explanation:
First, we need to expand the
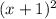 term.
term.
↓ rewriting the exponent as multiplication ...
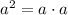
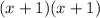
↓ rewriting using the distributive property ...
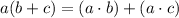
![\left[\frac{}{}(x+1) \cdot x\frac{}{}\right] + \left[\frac{}{}(x+1) \cdot 1\frac{}{}\right]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rgxftgke2kpos2w7z0mk9zdeqed60zyjle.png)
↓ simplifying using the distributive property
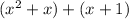
↓ combining like terms ...
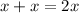
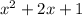
↓ putting into the equation for
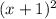
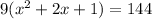
Next, we can simplify the left side (once again) using the distributive property.

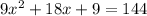
Then, we can get all the terms on one side by subtracting 144 from both sides.

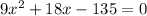
Finally, we can solve for x by factoring. To make this simpler, we can first factor out a 9 from each term on the left side.
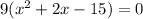
We can think about this as "undistributing", or reversing the distributive property:
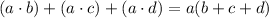
Next, we can factor the quadratic expression inside the parentheses using the rule:
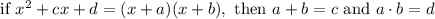
We can identify the following values for
 and
and
 :
:
So, the following equations must be true:
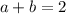 ,
,
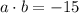
We can solve for
 and
and
 by listing out the factor pairs of
by listing out the factor pairs of
 and identifying the one whose factors add to
and identifying the one whose factors add to
 .
.
- (-15, 1) →
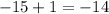 ❌
❌ - (-5, 3) →
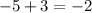 ❌
❌ - (-3, 5) →
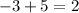 ✅
✅
So, we can determine the following values for
 and
and
 :
:
Hence, the factored form of the equation
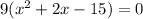 is:
is:
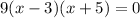
Now, we can solve for x using the zero product rule:

Therefore, the two solutions for x are:
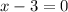 or
or
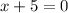
 or
or
