Answer:
3645π cubic units
Explanation:
To find the volume of the solid of revolution created by rotating the region bounded by the curve f(x) = -2x² + 12x + 54, x = 0, and y = 0 about the y-axis, we can use the method of cylindrical shells.
The volume of a solid of revolution using cylindrical shells is given by the integral:
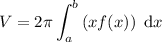
As the region is bounded by the x-axis and y-axis, we need to find the x-value where f(x) intersects the x-axis. To do this, set f(x) = 0 and solve for x:
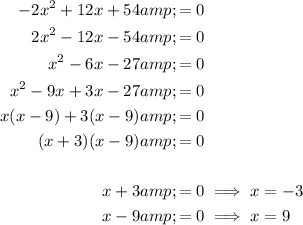
As the region is bounded by the x-axis and y-axis, the valid value of b is x = 9.
Therefore:
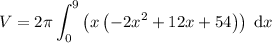
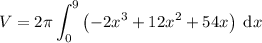
Integrate using the power rule: Increase the power by 1, then divide by the new power.
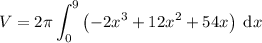
![V=2\pi \left[(-2x^(3+1))/(3+1)+(12x^(2+1))/(2+1)+(54x^(1+1))/(1+1)\right]_(0)^(9)](https://img.qammunity.org/2024/formulas/mathematics/college/ytdtd7qdl4tzq091oag47crzm9qlw7xfgn.png)
![V=2\pi \left[-(1)/(2)x^4+4x^3+27x^2\right]_(0)^(9)](https://img.qammunity.org/2024/formulas/mathematics/college/nvgqz5mjsb8i6fyqi875irl14os0n46d61.png)
Evaluate:
![V=2\pi \left[\left(-(1)/(2)(9)^4+4(9)^3+27(9)^2\right)-\left(-(1)/(2)(0)^4+4(0)^3+27(0)^2\right)\right]](https://img.qammunity.org/2024/formulas/mathematics/college/msh6umm8hc1fiam693h22xhkvy1fnnjun4.png)
![V=2\pi \left[(3645)/(2)-0\right]](https://img.qammunity.org/2024/formulas/mathematics/college/2s6wiq5j5ejscokf7nbgn71bt19ystrvkt.png)
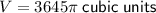
Therefore, the volume of the solid of revolution is 3645π cubic units.