Question

Heplllllllllllllllllllllllllllllllllllllllllllll

Answer 1

a) (1, 2)

b) (3, 1)

c)
`y = -(1)/(4)(x-1)^2 + 2`

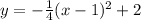
Explanation:

a) We can find the vertex of a parabola by looking for the point where the slope of the curve changes signs from positive to negative.

From the graph, we can identify this point as (1, 2).

b) We can see that some points on the parabola are (-2, 0), (-1, 1), and (3, 1).

c) We can find the equation of this parabola using vertex form:

`y = m(x-a)^2 + b`

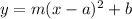
where
`(a, b)` is the vertex of the parabola and
`m` is the proportion of its vertical deviation from the standard parabola
`y=x^2`.

We already identified the vertex of the parabola as (1, 2), so we can assign the following variable values:

• 
  `a=1`
• 
  `b=2`

↓ plugging these into the vertex form equation

`y = m(x-1)^2 + 2`

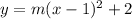
Next, we can solve for
`m` by looking at the point (3, 1). We can see that the vertical deviation is -1, whereas the deviation on a standard parabola 2 units to the right of the vertex is 4. We can identify the proportion between these two numbers as
`-(1)/(4)`.

↓ plugging this
`m`-value into the equation

`\boxed{y = -(1)/(4)(x-1)^2 + 2}`