Question

Find the standard deviation of the set of data. 11, 8, 6, 11, 24

Answer 1

Standard Deviation, σ: 6.2928530890209

Count, N: 5

Sum, Σx: 60

Mean, μ: 12

Variance, σ2: 39.6

Steps

σ2 =

Σ(xi - μ)2

N

=

(11 - 12)2 + ... + (24 - 12)2

5

=

198

5

= 39.6

σ = √39.6

= 6.2928530890209

Answer 2

Approximately 6.30

Step-by-step explanation:

Standard deviation is the square root of variance. It can be mathematically expressed as:

`\displaystyle{\text{SD} = \sqrt{(\sum \left(x - \bar x\right)^2)/(n) } }`

Where x is the data,
`\bar x` is the mean value of all data, and n is the number of data.

First, let's find the mean value (x bar):

`\displaystyle{\bar x = (\sum x)/(n)}\\\\\bar x = (11+8+6+11+24)/(5)}\\\\\displaystyle{\bar x = 12}`

So now, we have:

`\displaystyle{\text{SD} = \sqrt{(\sum \left(x - 12)^2)/(5) } }`

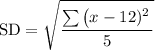
Input the data while also summing up the values:

`\displaystyle{\text{SD} = \sqrt{((11-12)^2+(8-12)^2+(6-12)^2+(11-12)^2+(24-12)^2)/(5) } }\\\\\displaystyle{\text{SD} = \sqrt{((-1)^2+(-4)^2+(-6)^2+(-1)^2+(12)^2)/(5)}}\\\\\displaystyle{\text{SD} = \sqrt{(1+16+36+1+144)/(5)}}\\\\\displaystyle{\text{SD} = \sqrt{(198)/(5)}}\\\\\displaystyle{\text{SD} = √(39.6)}\\\\\displaystyle{\text{SD} \approx 6.29285308902}`

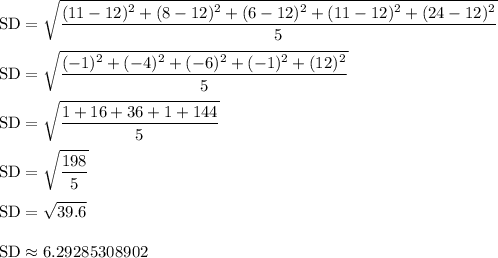
Therefore, the standard deviation is approximately 6.3. This is known as the population standard deviation.