Question

The remainder obtained when the polynomial g(t)= 2t³+at²-5t+1 is divided by t+2 is thrice the remainder obtained when g(f) is divided by t-1. Find;

* the value of a
* g(2)​

Answer 1

a = -1

g(2) = 3

Explanation:

Given polynomial:

`g(t)= 2t^3+at^2-5t+1`

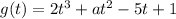
The remainder theorem states that when a polynomial p(x) is divided by a linear polynomial (x - c), then the remainder is equal to p(c).

Therefore, if the polynomial g(t) is divided by (t + 2), then the remainder is equal to g(-2):

`\begin{aligned}\textsf{Remainder:} \quad g(-2)&=2(-2)^3+a(-2)^2-5(-2)+1\\&=2(-8)+a(4)-5(-2)+1\\&=-16+4a+10+1\\&=4a-5\end{aligned}`

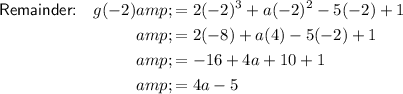
If the polynomial g(t) is divided by (t - 1), then the remainder is equal to g(1):

`\begin{aligned}\textsf{Remainder:} \quad g(1)&=2(1)^3+a(1)^2-5(1)+1\\&=2(1)+a(1)-5(1)+1\\&=2+a-5+1\\&=a-2\end{aligned}`

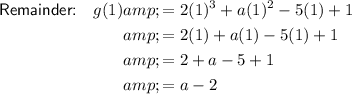
Given that the remainder (4a - 5) is three times the remainder (a - 2), then:

`\begin{aligned}4a-5&=3(a-2)\\4a-5&=3a-6\\4a-5-3a&=3a-6-3a\\a-5&=-6\\a-5+5&=-6+5\\a&=-1\end{aligned}`

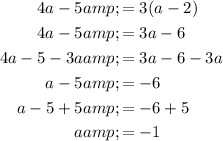
Therefore, the value of a = -1.

To find the value of g(2), substitute the found value of a = -1 into function g(t), then substitute t = 2 into the equation:

`g(t)= 2t^3+(-1)t^2-5t+1`

`g(t)= 2t^3-t^2-5t+1`

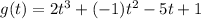
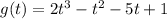
Therefore, the value of g(2) is:

`\begin{aligned}g(2)&= 2(2)^3-(2)^2-5(2)+1\\&= 2(8)-4-10+1\\&= 16-4-10+1\\&= 12-10+1\\&= 2+1\\&=3\end{aligned}`