Question

Can you please solve the OAB

Answer 1

3692.2 mm²

Explanation:

A major sector of a circle has a central angle greater than 180°, which means the major sector covers more than half of the entire circle.

Therefore, if OAB is the major sector, it is the pink shaded area in the given circle.

Angles around a point sum to 360°.

Therefore, the central angle of major sector OAB is:

`360^(\circ) - 67^(\circ) = 293^(\circ)`

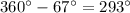
To calculate the area of major sector OAB, use the formula for the area of a sector.

`\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\left((\theta)/(360^(\circ))\right) \pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in degrees.\\\end{minipage}}`

The radius is r = 38 mm, and the central angle is θ = 293°.

Substitute these values into the formula and solve for A:

`A=\left((293^(\circ))/(360^(\circ))\right) \pi (38^2)`

`A=\left((293)/(360)\right) \pi (1444)`

`A=\left((293\cdot 1444)/(360)\right) \pi`

`A=\left((105773)/(90)\right) \pi`

`A=3692.17421...`

`A=3692.2\; \sf mm^2\;(1\;d.p.)`

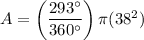
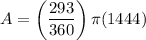
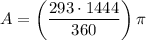
Therefore, the area of major sector OAB is 3692.2 mm², rounded to one decimal place.