Question

Sheena can row a boat at 3.00 mi/h in still water. She needs to cross a river that is 1.20 mi wide with a current flowing at 1.80 mi/h. Not having her calculator ready, she guesses that to go straight across, she should head upstream at an angle of 25.0° from the direction straight across the river. What is her speed with respect to the starting point on the bank?

Answer 1

Approximately
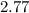`2.77` miles per hour.

Step-by-step explanation:

To find the resultant speed of the boat with respect to a fixed point on the ground, start by finding the resultant velocity of the boat in each one of the two orthogonal components: along the current and perpendicular to the current. Apply the Pythagorean Theorem to find the resultant speed of the boat from the velocity in the two components.

Let
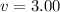`v = 3.00` miles per hour denote the velocity of the boat in water, and let
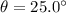`\theta = 25.0^(\circ)` denote the angle between this velocity and the direction perpendicular to the current.

Decompose the still-water velocity of the boat (with respect to the current) into two components perpendicular to one another: along the current and perpendicular to the current.

• Perpendicular to the current:
  `v\, \cos(\theta)`.
• Along the current:
  `v\, \sin(\theta)`.

The current affects the resultant velocity of the boat (with respect to the ground) only in the component along the current. It is given that the current flows at a rate of
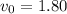`v_(0) = 1.80` miles per hour. Because the boat is travelling upstream against the current, the result velocity in the component along the current would be equal to the difference
`(v\, \sin(\theta) - v_(0))`.

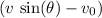Because the current does not affect the resultant velocity in the direction perpendicular to the current, component of the resultant velocity that direction to the current would be
`v\, \cos(\theta)`, same as that of the still-water velocity.

The resultant ground speed of the boat is equal to the magnitude of the resultant velocity, which can be found from the two orthogonal components using the Pythagorean Theorem:

`\begin{aligned}& \sqrt{(v\, \sin(\theta) - v_(0))^(2) + (v\, \cos(\theta))^(2)} \\ =\; & \sqrt{((3.00)\, \sin(25.0^(\circ)) - 1.80)^(2) + ((3.00)\, \sin(25.0^(\circ)))^(2)} \\ \approx \; & 2.77\end{aligned}`.

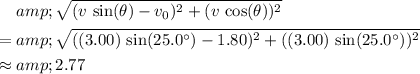In other words, the speed of the boat would be approximately
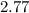`2.77` miles per hour with respect to a fixed point on the ground.