Question

Prove that 3+root 5 is an irratioonal number

Answer 1

Refer to the step-by-step explanation.

Explanation:

To prove that 3 + 2√5 is an irrational number, we need to show that it cannot be expressed as a ratio of two integers.
`\hrulefill`

Let's assume that 3 + 2√5 is rational, which means it can be expressed as a fraction of the form p/q, where p and q are integers with no common factors other than 1 and q ≠ 0.

So we have:

`\Longrightarrow3 + 2√(5) = \frac pq`

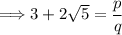
Rearranging the equation, we get:

`\Longrightarrow 2√(5) = \frac pq - 3`

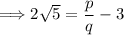
Squaring both sides to eliminate the square root, we have:

`\Longrightarrow (2√(5))^2 = \Big(\frac pq - 3\Big)^2\\\\\\\\\Longrightarrow 4(5) = \Big(\frac pq - 3\Big)^2\\\\\\\\\Longrightarrow 20 = \Big(\frac pq - 3\Big)^2`

Expanding the right side of the equation:

`\Longrightarrow 20 = \Big(\frac pq - 3\Big)\Big(\frac pq - 3\Big)\\\\\\\\\Longrightarrow 20 =(p^2)/(q^2)-3\frac pq - 3 \frac pq +9 \\\\\\\\\Longrightarrow 20 =(p^2)/(q^2)-6\frac pq +9`

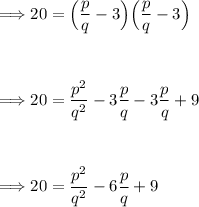
Multiplying both sides by q² to get rid of the denominator, we obtain:

`\Longrightarrow 20q^2 =p^2-6pq +9q^2`

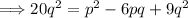
Rearranging the terms:

`\Longrightarrow p^2-6pq +(9q^2 -20q^2) =0`

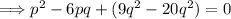
Simplifying further:

`\Longrightarrow p^2-6pq -11q^2 =0`

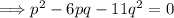
Now, let's consider this quadratic equation. If it has rational solutions for p and q, then its discriminant (b² - 4ac) must be a perfect square.

In this case, a = 1, b = -6, and c = -11. The discriminant is given by:

⇒ D = (-6)² - 4(1)(-11)

⇒ D = 36 + 44

∴ D = 80

Since 80 is not a perfect square, it means the discriminant is not a perfect square. Therefore, the quadratic equation does not have rational solutions for p and q.

Hence, our assumption that 3 + 2√5 is rational leads to a contradiction. Therefore, 3 + 2√5 must be an irrational number.
`\hrulefill`

Alternate method (A little easier):

We have:

`\Longrightarrow3 + 2√(5) = \frac pq`

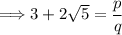
Multiplying each side of the equation by q:

`\Longrightarrow q(3 + 2√(5)) = p`

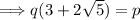
Expanding the left-hand side:

`\Longrightarrow 3q + 2q√(5) = p`

Subtracting each side of the equation by 3q:

`\Longrightarrow 2q√(5) = p -3q`

Dividing each side of the equation by 2q:

`\Longrightarrow √(5) = (p -3q)/(2q)`

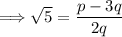
Given that (a - 3b)/2b is a rational number, it would imply that √5 is also rational. However, we know that √5 is irrational. Therefore, our initial assumption that 3 + 2√5 is rational is incorrect. Consequently, we can conclude that 3 + 2√5 is indeed an irrational number.