Question

For problems 1-4, solve the given system of equations using either substitution or elimination.

1.
2x + y = -8
y = 2x + 4

A. (-4, 0)
B. (-3, -2)
C. (1, 6)
D. Infinitely many solutions

2.
10x + 3y = -11
8x + 2y = -6

A. (-2, 3)
B. (-1, 1)
C. (1, -7)
D. No solution.

3.
-3x + 2y = 2
3x + 4y = 13

A. (1, 2. 5)
B. (2, 4)
C. No solution
D. Infinitely many solutions

4.
4x - y = -3
-8x + 2y = 6

A. (0, 3)
B. (-2, -5)
C. No solution
D. Infinitely many solutions

I've been trying to figure out these answers for an hour and I still don't understand it :( If anyone could please help out, it would really be appreciated <3​

Answer 1

Answer: 1: B, 2:C, 3:A, 4:D.

Explanation:

1.

2x + y = -8 (1)

y = 2x + 4 (2)

(2) 2x - y = -4

(1) 2x + y = -8 (add)

4x +0 = -12 (-y +y = 0)

`x= (-12)/(4)`

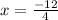
x = -3 {now put this value in eq (2)}

(2) y = 2(-3) + 4

y = -6+4

y = -2

(x, y) = (-3, -2)

2.

10x + 3y = -11 (1)

8x + 2y = -6 (2)

Multiply eq (1) by 2 & multiply eq(2) by -3

(1) 20x + 6y = -22

(2) -24x -6y = 18

-4x +0 = -4

`x = (-4)/(-4)`

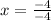
x = 1 {now put this value in eq1}

(1) 10(1) +3y = -11

3y = -11 -10

`y = (-21)/(3)`

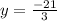
y = -7

(x, y) = (1, -7)

3.

-3x + 2y = 2 (1)

3x + 4y = 13 (2)

0 + 6y = 15

`y = (15)/(6)`

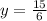
y = 2.5 ( now put this value in eq 1)

(1) -3x + 2(2.5) = 2

-3x + 5 = 2

-3x = 2 - 5

`x = (-3)/(-3)`

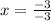
x = 1

(x, y) = (1, 2.5)

4.

4x - y = -3 (1)

-8x + 2y = 6 (2)

multiply eq (1) by 2

(1) 8x - 2y = -6

(2) -8x +2y = 6

Infinitely many solutions.

(An infinite solution has both sides equal & question 4 has both equations equal).