Question

Drag each tile to the correct box. triangle abc has these side measurements: ab = 17 bc = 18 ac = 21 order the angles of the triangle from largest measure to smallest measure. ?a ?b ?c

Answer 1

To order the angles of triangle ABC from largest measure to smallest measure, use the Law of Cosines to find the largest angle, which is opposite the longest side. Then, use subtraction to find the remaining angles.

Step-by-step explanation:

To order the angles of triangle ABC from largest measure to smallest measure, we need to find the largest angle first. We can use the Law of Cosines to find the largest angle, which is opposite the longest side. Let's calculate the angles:

• Angle C: Use the Law of Cosines to find angle C: cos(C) = (ab^2 + bc^2 - ac^2) / (2 * ab * bc). Substitute the given side measurements to find cos(C), then use the inverse cosine function to find angle C.
• Angle B: Use the Law of Cosines again, but this time, cos(B) = (ac^2 + bc^2 - ab^2) / (2 * ac * bc). Substitute the given side measurements to find cos(B), then use the inverse cosine function to find angle B.
• Angle A: Angle A is the remaining angle, which can be found by subtracting angle C and angle B from 180°.

Now, we can compare the angles and order them from largest to smallest measure.

Answer 2

The correct order of the angles of triangle ABC from largest measure to smallest measure is ∠B, ∠A, and ∠C.

In Mathematics, the length of the opposite side of a triangle would be largest when the interior angle facing it is the largest because the larger an angle, the more vertical the opposite side would become.

Conversely, the length of the opposite side of a triangle would be smallest when the interior angle facing it is the smallest because the smaller an angle, the less vertical the opposite side would become.

By applying the law of cosines, the measure of angle B is given by;

`b^2 = a^2 +c^2 -2ac CosB\\\\21^2 = 18^2 + 17^2-2(18)(17)CosB\\\\441=613-612CosB\\\\B=cos^(-1)((613-441)/(612) )`

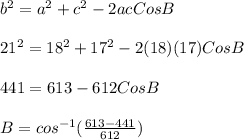
B = 73.6°.

For angle C, we have:

`c^2 = a^2 +b^2 -2ab CosC\\\\17^2 = 21^2 + 18^2-2(21)(18)CosC\\\\289=765-756CosC\\\\C=cos^(-1)((765-289)/(756) )`

C = 50.9°

By the triangle sum property, we have:

∠A + ∠B + ∠C = 180°

∠A = 180° - (50.9° + 73.6°)

∠A = 55.5°.

By critically observing the triangle shown below, we can logically deduce the following information:

The angle opposite a length of 17 is 50.9° ⇒ ∠C.

The angle opposite a length of 18 is 55.5° ⇒ ∠A.

The angle opposite a length of 21 is 73.6° ⇒ ∠B.

In this context, the correct order of the angles from largest measure to smallest measure is ∠B, ∠A, and ∠C.